コンテンツ

• 説明書
• どうやって
• 必要なもの

台形の体積の計算に含まれる数学的プロセスを理解することは、概念的および実用的な科学的構造の幾何学の中心を通ります。以下のテキストは、基本的な定式化の変数に付随する基本原理を最初に理解してから台形図形の問題を解決するために使用するためのステップバイステップの手順です。

説明書

台形の体積の計算に含まれる数学的プロセスを理解することは、概念的および実際的な科学的構造の幾何学の中心を通る （Fotolia.comからのjaddingtによる数学画像）

1. 住居用または商業用の建築物、泥床や住宅のパイプなどの土木工事、およびその他の施設などの実用的なプロジェクトの建設には、閉じた平面図内の液体物質の量に関する必要な知識が必要です。容積を計算する必要性の理解。既存の寸法を正確に測定することで、正確な体積計算が可能になります。

   実際には、地理的な盆地の粘土壁の断面として台形を見つけることは、台形を定義するのに役立ちます。四辺形の2辺が平行だが大きさが等しくなく、他の2辺が平行でない場合、この図は台形と呼ばれます。

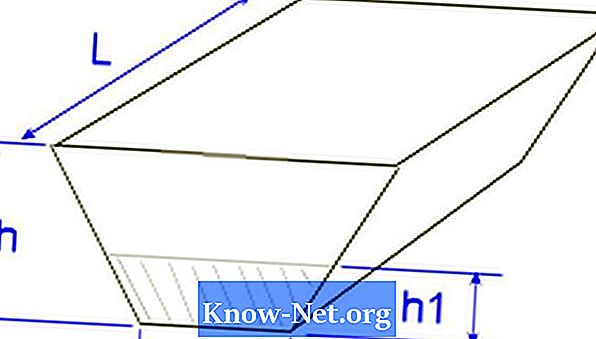
   したがって、長さが22.86 mの人物の場合、正面の寸法は幅17.37 m、高さ10.66 mで、底の幅21.94 m、3.65 mです。身長、体積の計算は次のようになります。

   1. この形状は、前面が17.37 x 22.86、長方形が底部に21.94 x 3.65、平面距離が22.86 mの長方形として考えることができます。

   2. このようにして体積を計算するための式は、前後の代わりに長方形の上下を持つトランクとして描くことができ、V = [a1b1 + a2b 2 +（a 1b 2 + a 2ここで、変数は、ａ １ ＝ １７，３７によって記述することができる。 ｂ１ ＝ １０．６６。 α２１ Ｄ ＝ ２１．９４。 ｂ２ ＝ ３．６５。 h = 22.86：V = [a 1b1 + a2b 2 +（a 1b 2 + a 2b1）/ 2] * h / 3 V = [17.37]10,66 + 21,943,65 + (17,373,65 + 21,94１０．６６）／ ２］×２２．８６ ／ ３Ｖ ＝ ［２６５．６０ ＋（６３．５４ ＋ ２３４．１１）／ ２］×７．６２Ｖ ＝ ［２６５．６０ ＋（２９７．６６）／ ２］ ] 7.62 V = [414.44] 7.62 V = 3158.03m³

      
      

2. 形式に従うと、台形の動的体積は静的モデルのものとは異なります。静的台形は幾何学的には2次元の図形であるためです。計算される面積は、紙の上に二次元で描かれた台形のものだけです。したがって、平均幅と平均長さを使用した式の代替バージョンは、次のとおりです。V = [a1b1 + a2b 2 + 4（（a 1 + a 2）/ 2 *（b 1 + b 2）/ 2）] * h / 6四角形の上辺と下辺の四辺の平均値となる辺があります。

3. ステップ２の動的適用のように作用して、プールまたは密閉された円筒のような台形構造の容積は、特定の高さのメートル当たりのリットルとして計算することができる。これは、満杯のコンテナの容積をその高さで割ったものが適切な比率になることを意味します - 立方メートルを得るために式を使ってください（mの寸法で）。

   円筒形ではない容器については、生徒が望むなら、比率は深さによって変わります。そしてこれは、コンテナが部分的にいっぱいになり、ボリュームがさまざまなレベルで決定されることを意味すると考えるかもしれません。つまり、音量は高さの関数です。

4. もう少し詳しく言うと、「ａ」方向の幅がａ１からａ２まで直線的に変化するにつれて、ａ ＝ ａ１ ＋（ａ２ − ａ１）ｋ ＝（１ − ｋ）ａ１ ＋ ｋａ２となる。どのユニットkhが下から上がるか（kは0から1の範囲）同様に、ｂ ＝ ｂ１ ＋（ｂ２ − ｂ１）ｋ ＝（１ − ｋ）ｂ１ ＋ ｋｂ２である。高さkh、底辺a1×b1、頂部a×bのソリッドの体積はV（k）= [a1b1 + ab + a1b / 2 + aｂ１ ／ ２］ ＊ ｋｈ ／ ３。

   比kの代わりに実液位を使用すると、k = L / hを代入することができ、V（L）= [（3h ^ 2-3Lh + L ^ 2）a1が得られます。b1 + L2a2a2b 2 +（3Lh - 2L 2）（a 1b 2 + a 2ｂ１）／ ２］ ＊ Ｌ ／（３ｈ ＾ ２）。これは私たちに深さの関数としての音量を与えます。

   
   

5. 台形の体積を適切に計算することは、台形が二次元か三次元かを解釈する能力を含む。台形解釈工学的側面の動的な実践は、台形図形が単純に描かれたものか構築されたものであるか、それが紙の上のボリュームまたは単なるスケッチを含むかどうかを中心に展開します。

どうやって

• 幾何学的問題を解くことによって、学生は式がどのようにそしてなぜそのようになっているのか、そしてなぜ身長がそれほど重要な変数であるのかを理解することができます。たとえば、Hewlett-Packardの科学計算用電卓を使用して手動で取得した回答を確認することは、完全な正確さを達成するための良い方法です。

必要なもの

• えんぴつ
• ノートのシート（線の有無にかかわらず）
• 定規